What Makes Recognizing Continuous Speech More Di Cult Than Recognizing Isolated Words
Introduction
In recent decades, a lot of research has been done in enhancing the robustness of speech recognition (SR) in a noisy environment. Due to the inherent variability of the speech signal and random nature of noise, a tradeoff has to be made in speech distortion and noise reduction in speech enhancement techniques. The latest development in digital signal processing (DSP) technology is utilized as a part of various application regions of speech processing like signal compression, improvement, synthesis, and recognition (Rabiner & Schafer, 2005; Rabiner & Juang, 1999).
Speech is a standout amongst the most critical and characteristic means for humans to communicate their feelings, intellectual states, and aims to each other. The feature extraction procedure extracts some of the popular features like mel-frequency spectra and perceptual linear prediction (PLP) coefficients. The features can also be extracted using a rectangular equivalent bandwidth (ERB) to increase the rate of speech recognition (Oh & Chung, 2014). Amplitude modulation spectrogram (AMS) design has also been used for speech recognition for increasing its performance by noise attenuation (Ma & Zhou, 2008). A spoken word recognition system empowers a computer to understand the words spoken by changing over to text form. The paper (Kamalvir & Neelu, 2015) acquaints the reader with the procedure and strategies of isolated word recognition systems. It gives a succinct review of methods utilized amid different phases of the spoken word recognition system. The utility and advantages of every method are examined quickly.
Numerous investigators (Aquino et al., 2020; Chiang et al., 2019; de Jesús Rubio 2010; Dhanashri & Dhonde, 2017; Meda-Campaña 2018, Jain & Shukla, 2019) have developed new learning algorithms. The Levenberg–Marquardt (LM) algorithm (Nawi et al., 2013) is derived from Newton's Technique. In this algorithm, both the gradient and the Jacobian matrix are computed.
In (Elias et al., 2020), the Hessian, which is the second cost map derivative, is combined with a mini-batch to tune the neural networks. Since the closest approximation is obtained between the outputs of the neural network and the lowest value of the cost map, the authors have found the best agreement with Hessian with the mini-batch (HDMB) technique compared to the steepest descent (SD), SD with mini-batch and Hessian. HDMB first initializes the scaling parameters between 0 and 1, and after forward propagation, the cost map is obtained. The backpropagation then proceeds and finally tuning of the neural network is done by finding the second derivative. The authors have successfully applied HDMB in predicting electrical demand.
A deep evolving denoising autoencoder (DEVDAN) has been suggested by Ashfahani et al. (2020). In the propagative stage and the discriminative stage, it designs a disclosed structure where the concealed elements can be spontaneously added and quickly rejected as necessary. The generative stage uses unlabeled details to strengthen the prognostic act of the discriminative model. Besides, DEVDAN is open to the problem-specific verge and entirely works in the learning fashion of a single pass. Various optimization techniques have been used to increase the efficiency of designs by choosing the best solution among various viable solutions in different domains (Jain et al., 2012, 2013; Shukla & Jain, 2020). For enhancing speech recognition and finding out the familiarity of the words the improved particle swarm optimization (IPSO) algorithm along with a hidden Markov model (HMM) is suggested in (Selvaraj & Balakrishnan, 2014). Another training algorithm was developed based on a whale optimization algorithm (WOA) which could understand an extensive variety of optimization issues and outperform the present algorithms (Mirjalili & Lewis, 2016).
Different techniques have been proposed for SR by various researchers, it is observed that they have the limitation of poor recognition accuracy for real-time data and higher computational time (Shukla et al., 2019). The main attraction of the proposed system is its speed and efficiency for standard data set (Garofolo et al., 1993) as well as real-time data. This paper is an extended version of (Shukla & Jain, 2019) in which the opposition artificial bee colony (OABC) optimization technique has been applied for optimizing the hidden layers of artificial neural network (ANN). In that work, the AMS technique is used for feature extraction then the LM algorithm is used for quick and productive training. To make the proposed system more efficient, the ANN structure is redesigned using the OABC optimization algorithm.
In this paper, instead of OABC, the opposition whale optimization algorithm (OWOA) is applied for optimizing the hidden layers and neurons of DNN. A more deep structure is used and it is resilient to the noises present. With the current coronavirus pandemic (COVID) conditions prevailing the speech recognition system will be used at most of the places in the future from being the part of security system to our daily appliances, all will be operated by speech command. So the proposed SDRN system will be very beneficial. The organization of this paper is as follows: The proposed methodology related to speech recognition is given in Sect. 2. Section 3 describes the results and comparison with existing methods and Sect. 4 concludes the proposed work.
Proposed methodology
In existing works, for converting the isolated active word speech into text, various techniques were utilized and performed. The proposed SDRN uses handcrafted features. The AMS technique is used to extract the features from the input speech signal. Then the extracted input features are taken into DNN for training and testing. The hidden layers of DNN its neurons are optimized using the OWOA optimization technique and this proposed method is referred to as a neural-based opposition whale optimization algorithm (NOWOA) in this paper. The OWOA algorithm is the latest optimization algorithm proposed by (Alamri et al., 2018). It is an efficient algorithm used in research areas like solar cell diode modeling (Abd Elaziz and Oliva 2018).
Whales are considered to be significantly wise animals. WOA is the latest developed optimization technique that mimics the common activities of the humpback whales. This algorithm has a better accuracy level, and for more enhancements, the opposition algorithm is included.
In this work, 375 features of input speech signals are used as input to the DNN. Two types of databases have been used in this work namely standard database and real-time database. For the standard database, the TIMIT (Garofolo et al., 1993) corpus of reading speech has been used. This database was developed to offer voice data for acoustic and for the studies of phonetic data for automated speech recognition systems. It consists of vast soundtracks of 630 narrators of 8 main vernacular divisions of the United States. The TIMIT corpus contains a total of 6300 statements, 10 sentences spoken by each of those narrators. For each statement, a 16 kHz speech waveform file has been used. The core test set contains 192 different texts. The chosen texts were monitored for the existence of at least one phoneme. Figure 1 describes the conceptual methodology of the proposed system.
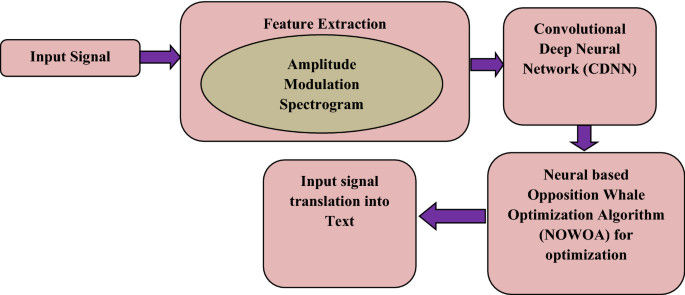
Block diagram of a conceptual methodology of the proposed system
Among these 6300 speech signals, 70% are utilized for training and the remaining 30% are used for testing. For validation purposes, 60 isolated (real-time) speech signals are recorded in ambient conditions, among which 70% are used for training and the remaining 30% are used for testing. For validation of continuous (real-time) speech signals, 110 speech signals were considered, out of which 70% are used for training and the remaining 30% are used for testing. Then, 375 features are mined from these speech signals. Initially, features are taken out from the input speech corpus using AMS. The input is a combination of clean and noisy signals and it is pre-processed by normalizing, quantizing, and windowing.
The acquired signals have been disintegrated into different time–frequency (TF) units by utilizing bandpass filters which will transform the signals within a specified frequency range. The signals are split into 25 TF units each attached to a channel Ci, where i = 1, 2, 3…25. Among these, 25 bands of channels are considered and the signal frequencies are characterized in the range of the individual channel.
Let the feature vector (FV) be denoted by a fr (λ,φ) where φ is the time slot and λ is the sub-band. By considering the small updates in TF domains, we additionally consider the functions Δa ti to the extracted features, given beneath, where ti is the time, and B is the channel bandwidth.
$$\begin{gathered} \Delta a_{ti}\, (\lambda ,\varphi ) = a_{fr} \,(\lambda ,\varphi ) - a_{fr}\, (\lambda,\varphi - 1 ),\,\, \hfill \\ \,where\,\,\varphi = 2,...ti \hfill \\ \end{gathered}$$
(1)
The frequency delta function Δa d is given as:
$$\begin{gathered} \Delta a_{d} (\lambda ,\varphi ) = a_{fr} (\lambda ,\varphi ) - a_{fr} (\lambda - 1,\varphi ),\,\, \hfill \\ \,where\,\,\lambda = 2,...{\text{B}} \hfill \\ \end{gathered}$$
(2)
The cumulative FV a (λ,φ) can be defined as:
$$a(\lambda ,\varphi ) = [a_{fr} (\lambda ,\varphi ),\,\,\Delta a_{ti} (\lambda ,\varphi ),\,\,\Delta a_{d} (\lambda ,\varphi )]$$
(3)
In this way, the features are extracted from the input speech signal using the AMS technique, which will be then used as input for DNN.
Deep neural network
A DNN is a network with a fixed level of intricacy and with diverse layers. DNN uses a complex technical exemplary for managing the data in an erratic mode. DNN with plentiful layers typically combines the characteristic removal and organization procedure into a signal learning body. These kinds of NN have attained achievement in multifaceted areas for the documentation of designs in contemporary ages. The network consists of a layer of inputs, HL, and OL. The input layer is taken as layer 0 for a P + 1 layer DNN framework and the output layer is P for P + 1 layer DNN as given in Eq. 4 and Eq. 5.
$${{\varvec{x}}}^{p}=f\left({{\varvec{y}}}^{p}\right)=f\left({{\varvec{W}}}^{p}{{\varvec{x}}}^{p-1}+{{\varvec{b}}}^{p}\right), 0<p<P$$
(4)
$${{\varvec{y}}}^{p}={{\varvec{W}}}^{p}{{\varvec{x}}}^{p-1}+$$
(5)
The activation vector and the excitation vector are x andy respectively, andW gives the weight matrix and b is the bias vector.
Stochastic feed-forward backpropagation (Bengio, 2012; LeCun et al., 2012) is used for learning the weights of DNN. The difference between each output and its target value is transformed into an error derivative. Then error derivatives from error derivatives in the above layer are measured in each hidden layer. Then error derivatives w.r.t. activities are used to obtain error derivatives w.r.t. incoming weights in Eq. 6–9. Here e is the error, y' is the target value and y is the output.
$$\begin{gathered} e_{{}} = \frac{1}{2}\sum\limits_{j \in output} {\;(y^{\prime}_{j} } - y_{j} )^{2} \hfill \\ \frac{{\partial e_{{}} }}{{\partial y_{j} }} = - (y^{\prime}_{j} - y_{j} ) \hfill \\ \end{gathered}$$
(6)
$$\frac{\partial e}{{\partial x_{j} }}\;\; = \;\;\frac{{dy_{j} }}{{dx_{j} }}\;\frac{\partial E}{{\partial y_{j} }}\;\; = \;\;y_{j} \;(1 - y_{j} )\;\frac{\partial e}{{\partial y_{j} }}$$
(7)
$$\frac{\partial e}{{\partial y_{i} }}\;\; = \;\;\sum\limits_{j} {\frac{{dx_{j} }}{{dy_{i} }}\frac{\partial E}{{\partial x_{j} }}} \;\; = \;\;\sum\limits_{j} {w_{ij} \frac{\partial E}{{\partial x_{j} }}}$$
(8)
$$\frac{\partial e}{{\partial w_{ij} }}\;\; = \;\;\frac{{\partial x_{j} }}{{\partial w_{ij} }}\;\;\frac{\partial E}{{\partial x_{j} }}\;\; = \;\;y_{i} \frac{\partial e}{{\partial x_{j} }}$$
(9)
Convolutional neural network
CNN is a group of profound learning neural networks.
A CNN has
-
Convolutional layer
-
ReLU layer
-
Pooling layer
-
Fully connected layer
Convolutional layers use an intricacy action to the input. This permits the data on to the subsequent layer. Assembling pools the outputs of groups of neurons into a distinct neuron in the following layer. Completely associated layers join each neuron in a single layer to each neuron in the succeeding layer.
CNN architecture
A definitive CNN (Abdel-Hamid et al., 2014) design would appear somewhat similar to this. Figure 2 exemplifies CNN architecture showing layers containing a couple of convolution layers and a pooling layer in series, where charting from either the input layer or pooling to a convolution layer.
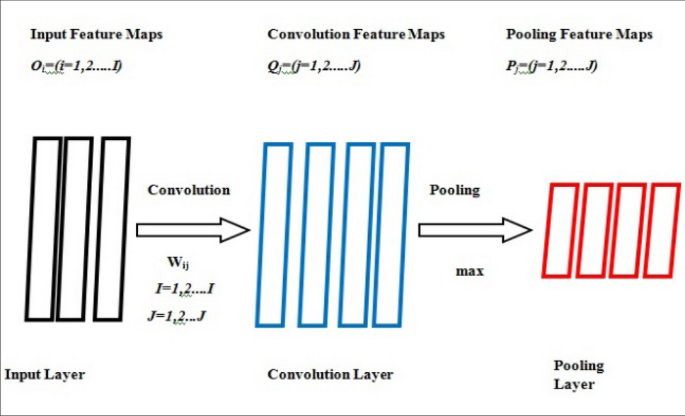
CNN architecture
When the charts of the input feature are made, the layers of convolution and pooling use their relating actions to make the training of the elements in those layers. The elements of the convolution and pooling layers can also be prearranged into charts, like that of the input layer. A few convolution and pooling layers in series are typically mentioned in CNN lexis as a unique "layer" of CNN. Thus a deep CNN contains two or more of these couples in series.
The convolution layer unit of one feature map can be calculated as:
$${l}_{s,m=}\sigma \sum_{i=1}^{p}\sum_{n=1}^{F}{I}_{i,n+m-1}{w}_{i,s,n}{w}_{I,s }$$
(10)
$$(s=\mathrm{1,2}\dots ..,S)$$
where I i,m is the mth unit of the ith input feature map, l s,m is the mth element of the jth feature chart in the convolution layer, w i,s,n is the nth component of the mass trajectory, which joins the ith input feature chart to the feature chart of the convolution layer. F is named the filter dimension, which regulates the amount of the filter bands in every input feature chart that every feature in the convolution layer gets as an input. As a result of the area that ascends from our opinion of mel frequency spectral coefficients (MFSC) aspects, these feature charts are limited to a partial incidence range of the speech signal. Using max pooling function the pooling layer in CNN is given as
$${p}_{i,m}={max}_{n=1}^{G}{q}_{i\left(m-1\right)Xs+n}$$
(11)
where G represents the pooling size, and, s denotes the shift size that determines the overlap of adjacent pooling windows. The output layer in CNN is
$${p}_{i,m}=x\sum_{n=1}^{G}{q}_{i\left(m-1\right)Xs+n}$$
(12)
where x represents the scaling factor that can be learned. In the image, identification uses with the limitation that G =s and if the assembling windows do not overlay and have no places between them, it has been recognized that max-pooling performs better than average-pooling.
CNN algorithm
- 1.
Initiates with an input speech signal.
- 2.
Puts on numerous diverse filters to it to generate a feature chart.
- 3.
Puts on a rectified linear unit (ReLU) function to upsurge non-linearity.
- 4.
Uses a pooling layer to every feature chart.
- 5.
Inputs the trajectory into a completely associated profound neural network.
- 6.
Practices the structures via the network.
- 7.
The last completely associated layer offers the "voting" of the groups.
- 8.
Trains via onward proliferation and back proliferation for several, various eras.
- 9.
This procedure reprises till a definite neural network with trained masses and feature indicators is got.
But since CNN is needed to measure the performance for each frame for decoding, pooling or shifting size may influence the fine resolution of deeper CNN layers, and a broad pooling size can affect the localization of the state labels. This can induce phonetic confusion, particularly at the boundaries of segments. Such a good one pool size must be picked.
Optimizing DNN hidden layers and its neurons
The optimization of DNN layers and their neurons is done here using distinctive algorithms namely, Whale Optimization Algorithm (WOA), Ant Bee Colony (ABC), Genetic Algorithm (GA), Particle Swarm Optimization (PSO), and OWOA are used. In this procedure, for maximum recognition accuracy, the WOA algorithm is altered here as OWOA.
Opposition whale optimization algorithm
In many optimization techniques, initial solutions are generated randomly in the permissible domain. However, a randomly initialized solution may occur in the opposite direction of the best solution, which will unnecessarily increase the computational cost. Therefore a similar idea of opposition-based initialization known as OWOA is applied as shown in the flowchart Fig. 3.
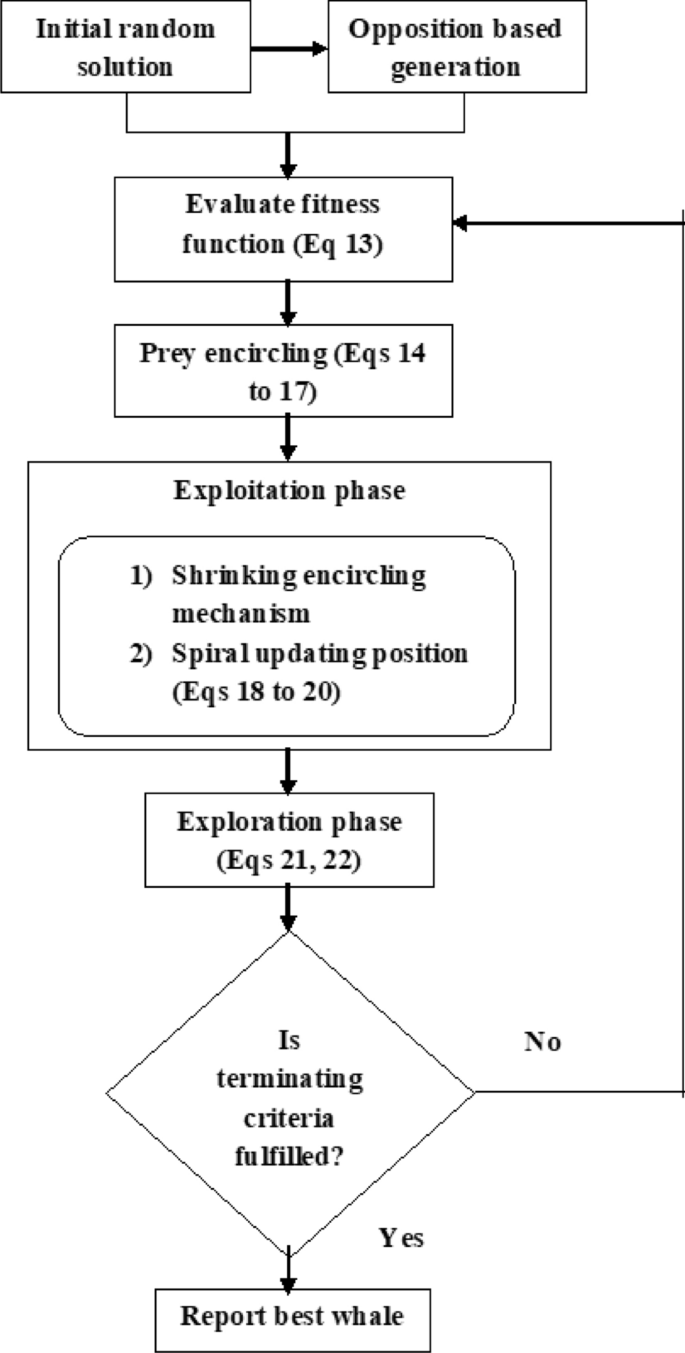
OWOA flowchart
Original solution creation
The initial solution is produced arbitrarily with the hidden layer (HL) from 1 to 5 and the corresponding neurons from 1 to 30. The process of generating the initial solution has been described in detail in our previous work (Shukla et al., 2019).
Fitness computation
The fitness function (f i ) is computed as
$$f_{i} = \frac{Correctly\,predicted\,\,data}{{Total\,\,\,data}}$$
(13)
Based on this fitness function, each NN structure is redesigned and the output is predicted.
Whale optimization algorithm
In WOA, a random agent is used for searching the solution space for the prey. It additionally poses the capacity to create bubble-net connecting techniques by utilizing spirals. WOA incorporates three operations: (i) encircling the prey (ii) exploitation (iii) exploration.
The mathematical formulation is modeled below:
(1) Prey encircling: In this step, initially an optimum agent is assumed which has the best location of the prey for the current solution. The remaining agents consequently update their regions towards the best search agent by applying the below equations:
$$\vec{D} = \left| {\vec{C}.\,\vec{P}^{ * } (t) - \mathop{P}\limits^{\rightharpoonup} (t)} \right|$$
(14)
$$\vec{P}(t + 1) = \vec{P}^{ * } (t) - \vec{A}.\,\vec{D}$$
(15)
where \(\vec{D}\) is the distance between the whale and prey, t is the current iteration, \(\vec{A}\) and \(\vec{C}\) are coefficient vectors.
\(\vec{P}^{ * }\) is the position vector of the best solution acquired until now and \(\vec{P}\) is the location vector. In the event of the presence of an optimum solution, \(P^{ * }\) it needs to be updated in each iteration.
\(\vec{A}\) and \(\vec{C}\) can be derived as:
$$\vec{A} = 2\vec{a}.\vec{r} - \vec{a}$$
(16)
$$\vec{C} = 2.\vec{r}$$
(17)
where the parameter \(\vec{a}\) is reduced sequentially from 2 to 0 at each iteration and \(\vec{r}\) is a vector in the range of [0, 1].
(2) Exploitation or Bubble-net connecting: This phase contains the following two methods:
By setting the random value of \(\vec{A}\) in the range [− 1, 1], the new location of the agent can be found somewhere in the middle of the past location and the present best location of the agent.
• Position updating using Spirals: Here, the distance between the whale located at (P, Q) and its prey located at (\(P^{ * }\), \(Q^{ * }\)) is computed and then a spiral equation is derived to recreate the mobility of the whales.
$$\vec{P}(t + 1) = \vec{D}^{^{\prime}} .e^{bl} .\cos (2\pi l) + \vec{P}^{ * } (t)$$
(18)
$$\vec{D}^{^{\prime}} = \left| {\vec{P}^{ * } (t) - \vec{P}(t)} \right|$$
(19)
Equation (19) is used to compute the distance of the ith whale to the prey (optimum solution accomplished up until now), b is constant which decides the spiral shape and l is in the range of [− 1, 1]. The whale moves towards its prey simultaneously by shrinking encircling in a spiral-shaped trajectory. The whale moves towards its prey simultaneously in a shrinking encircling and spiral-shaped path. In this manner there is a 50% chance of switching between the two modes to update its next position is modeled as follows:
$$\vec{P}(t + 1) = \left\{ {\begin{array}{*{20}l} {\vec{P}^{*} (t) - \vec{A}.{\mkern 1mu} \vec{D}} & {if\;p{\text{ }} < {\text{ }}0.5} \\ {\vec{D}^{\prime}.e^{{bl}} .\cos (2\pi l) + \vec{P}^{*} (t)} & {if\;p \ge 0.5,} \\ \end{array} } \right.$$
(20)
where p is a random number in [0, 1].
(3) Exploration: In this phase, \(\vec{A}\) it is set between [− 1, 1] to make the agents step away from the candidate whale by keeping its value either greater than 1 or less than − 1. The position of the agent is updated based on the randomly selected search agent instead of the optimum search agent and keeping,\(\vec{A}\) between [− 1, 1] promotes WOA to accomplish a global search. The modeling of this mechanism is given below:
$$\vec{D} = \left| {\vec{C}.\,\vec{P}_{rand} - \vec{P}\,} \right|$$
(21)
$$\vec{P}(t + 1) = \vec{P}_{rand} - \vec{A}.\,\vec{D},$$
(22)
where \(\vec{P}_{rand}\) is a random location vector of a random whale that is selected from the present population.
The speech recognition problem is sorted out by utilizing the DNN technique but certain issues limit its performance. This contemplates the urge to enhance the performance of the DNN technique by incorporating optimization algorithms for redesigning its structure. There are different optimization techniques amid, WOA that have a significant impact on solving nonlinear problems. WOA technique is utilized here to redesign the DNN structure, this unveils appropriate performance over existing methodologies. To further enhance performance opposition methodology is used in WOA. A brief description of other algorithms is provided below:
Artificial Bee Colony (ABC) optimization In this optimization technique, the normal behaviors of honey bees are copied in search of a better solution. There are 3 types of honey bees involved in ABC (Karaboga & Basturk, 2007) (i) scout bees which search for food sources randomly (ii) employed bees which share the location of food sources with onlooker bees (iii) onlooker bees which estimate the fitness function and select the optimum food source based on it.
Particle swarm optimization (PSO) It is a population-based optimization method (Zhou et al., 2003) replicated from the communal deeds of particles. Every particle has a location in the multi-dimensional solution space of the source. The positioning of a particle is calculated among many swarms according to its own personal best experience of a particle (Pbest) and the general best experience (Gbest). PSO position and velocity are modified for each particle in every iteration according to simple mechanisms.
Genetic Algorithm (GA) It is a technique applied for handling conditional and unconditional optimization problems (Harik et al., 1999) that are based on natural choice. It performs the operations mutation, crossover, selection, etc. to provide accurate solutions for the optimization problems.
Results and discussion
In the speech recognition procedure, the TIMIT corpus (Garofolo et al., 1993) of reading speech has been used. It contains wide recordings of 630 speakers of eight major dialects of American English. The NOWOA optimization algorithm is compared with other optimization algorithms WOA, ABC, GA, and PSO.
For these five algorithms, the classification graph is plotted with performance assessment criteria:
- a)
Accuracy
- b)
Sensitivity
- c)
Specificity
- d)
Positive predictive value (PPV)
- e)
Negative predictive value (NPV)
- f)
False-positive rate (FPR)
- g)
False-negative rate (FNR)
- h)
False discovery rate (FDR)
DNN structures for isolated and continuous speech signals
Based on the database, each of the employed optimization technique predicts the appropriate DNN structure for maximum recognition accuracy. The corresponding details of predicted DNN structures have been summarized in Tables 1, 2, and 3. It shows the number of neurons in each HL of the DNN structure for each of the optimization techniques.
From these tables, it can be seen that the proposed NOWOA method has a comparatively less number of hidden layers and the optimization of neurons is done for best recognition accuracy. The result clearly shows that for any kind of dataset (real-time) the structure of DNN can be redesigned using NOWOA for maximum recognition by properly training and testing.
The training times utilized in the algorithms are shown in Table 4.
Table 4 shows that NOWOA consumes less training time when than the other algorithms. Hence it reduces the time, cost and enhances the speed of recognition.
The performance assessment is carried out by calculating the following metrics:
$$\left. {\begin{array}{*{20}l} {Sensitivity = \frac{{tp}}{{tp + fn}}} \\ {Specificity = \frac{{tn}}{{tn + fp}}} \\ {Accuracy = \frac{{(tp + tn)}}{{tp + tn + fp + fn}}} \\ \end{array} } \right\}$$
(23)
where,
tp: True Positive- predicts the appropriately detected signal as the desired signal.
tn: True Negative -predicts the appropriately detected signal as the undesired signal.
fp: False Positive—predicts the inappropriately detected signal as the desired signal.
fn: False Negative- predicts inappropriately detected signal as an undesired signal.
A confusion matrix represents the performance of a classifier on test data in terms of tp, tp, fn, and tn. The results for 240 testing data are presented in Table 5. The following table describes the example of a confusion matrix for isolated speech. Ten words are shown and each word is in 8 dialects. The result shows that the system recognizes the actual word with maximum accuracy (tp and tn values). Some similar dialects give fp and fn values also. By thoroughly training the DNN these errors can be further minimized.
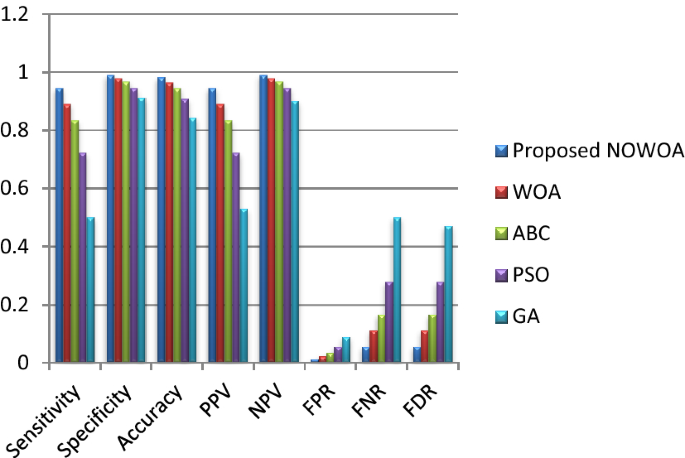
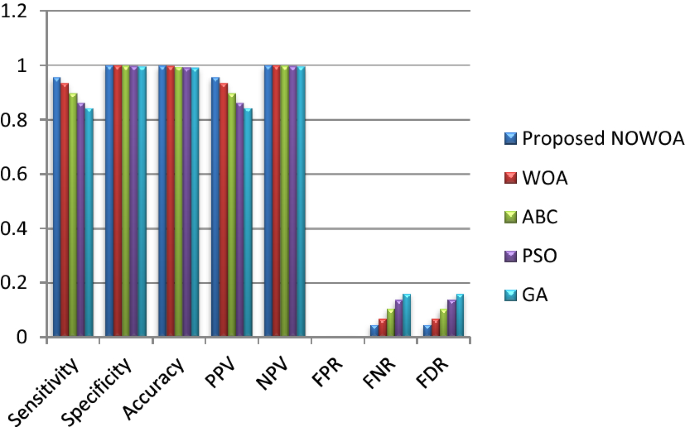
The proposed NOWOA algorithm is compared with the existing algorithms. The prediction output for isolated (real-time), isolated (standard database), and continuous (real-time) signals are shown in Figs. 4, 5, and 6 respectively.
Prediction outputs for isolated signals (real-time)
Prediction outputs for isolated signals (standard)
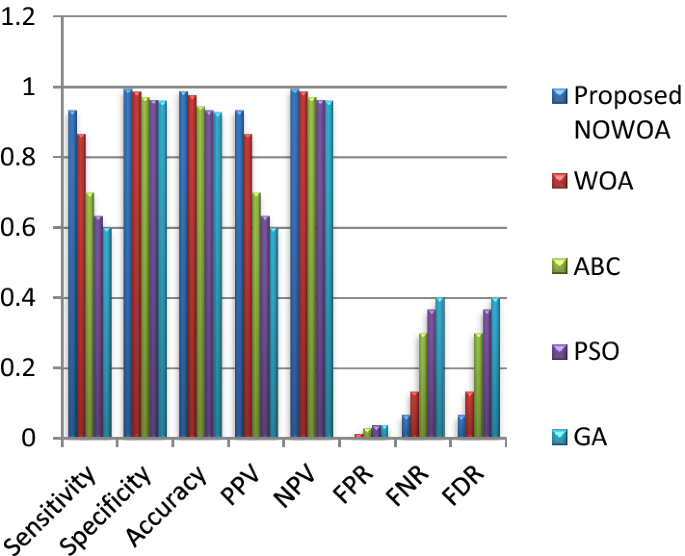
Prediction outputs for continuous signals (real-time)
Figure 4 shows the performance of NOWOA on isolated signal (real-time investigation). It exhibits superior over other employed techniques. The excellent performance of the proposed method is accomplished in all evaluated measures, which is possible because of the neural-based opposition strategy. In terms of accuracy, NOWOA obtained 98.1%, which is 1.9% better than WOA, 3.7% better than ABC, 7.4% greater than PSO, and 13.9% greater than least performing GA. In contrast with other optimization methods, NOWOA also showcases excellent performance in other standard measures. Accuracy is the degree to which the result of measurement reveals the performance of employed techniques.
Figure 5 shows the performance of NOWOA on standard-database for isolated signal evaluation is greater than that of other techniques used. In terms of accuracy, NOWOA obtained 99.6%, which is 0.1% better than WOA, 0.3% better than ABC, 0.6% greater than PSO, and 0.7% greater than minimum performing GA. Likewise, NOWOA exposes more excellent performance in other measures when compared with other employed techniques.
Figure 6 gives the performance of NOWOA on continuous signal real-time-database investigation exhibits greater than other employed techniques. The excellent performance of proposed methods accomplished in all evaluated measures, which is possible because of the neural-based opposition strategy. In terms of accuracy, NOWOA obtained 99.6%, which is 1.2% better than WOA, 4.2% better than ABC, 5.4% greater than PSO, and 6% greater than minimum performing GA. Likewise, NOWOA exposes more excellent performance in other measures when compared with other employed techniques.
Performance of NOWOA with other algorithms
This section presents the performance results comparison of NOWOA with that of HMM-based speech recognition system (Ananthi & Dhanalakshmi, 2013) and VAD (Ali & Talha, 2018) method for isolated words (standard TIMIT database). Figure 7 shows the results for these 3 algorithms. Figure 7 shows the performance comparison for isolated signals (standard) for NOWOA, HMM, and VAD. As seen from Fig. 7, NOWOA outperforms both HMM and VAD by attaining a sensitivity of 0.933 whereas HMM and VAD have sensitivity 0.906 and 0.892, respectively.
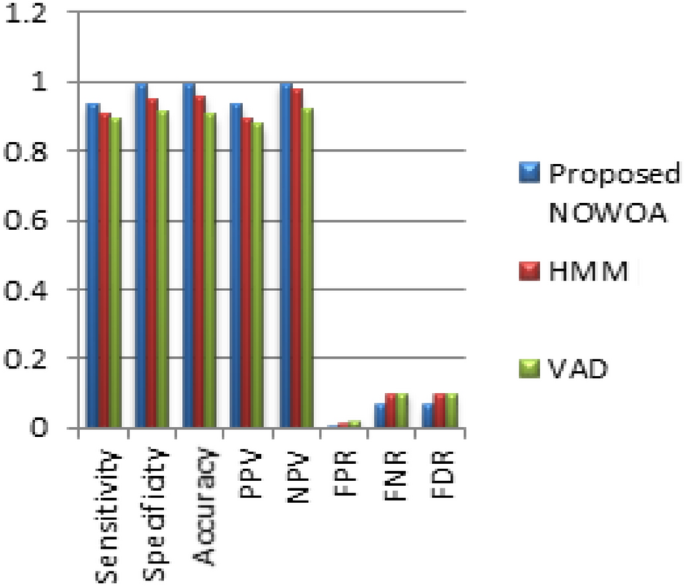
Performance comparison of NOWOA, VAD (Ali & Talha, 2018), and HMM (Ananthi & Dhanalakshmi, 2013) for isolated words
NOWOA has a specificity of 0.993 and HMM and VAD have a specificity of 0.946 and 0.913. NOWOA has an accuracy of 0.987 whereas the accuracy of HMM and VAD are 0.957 and 0.904. Similarly, NOWOA has achieved the highest values for PPV and NPV. In terms of the metrics FPR, FNR, and FDR, NOWOA has attained an average percentage improvement of 38% and 43% over HMM and VAD, respectively.
Conclusion
The novelty of the proposed SDRN is in optimizing the neural network structure (hidden layer and its neurons) and including NOWOA. This paper recognizes the isolated words and continuous speech signals and converts them into text. For this, different speech signals are taken, and feature extraction is performed by applying AMS. In this work, the accuracy value of NOWOA for isolated signals (real-time) is 98.1%, isolated signals (standard) are 99.6% and continuous signals (real-time) are 98.7%. The acquired outcome demonstrates that NOWOA determines the optimal combination of features with high classification accuracy. The proposed technique shows better performance concerning other optimization techniques. In future work, this technique can be associated with different speech recognition systems to improve efficiency further.
References
-
Abd Elaziz, M., & Oliva, D. (2018). Parameter estimation of solar cells diode models by an improved opposition-based whale optimization algorithm. Energy Conversion and Management, 171, 1843–1859.
-
Abdel-Hamid, O., Mohamed, A. R., Jiang, H., Deng, L., Penn, G., & Yu, D. (2014). Convolutional neural networks for speech recognition. IEEE/ACM Transactions on Audio, Speech, and Language Processing, 22(10), 1533–1545.
-
Alamri, H. S., Alsariera, Y. A., & Zamli, K. Z. (2018). Opposition-based whale optimization algorithm. Advanced Science Letters, 24(10), 7461–7464.
-
Ali, Z., & Talha, M. (2018). Innovative method for unsupervised voice activity detection and classification of audio segments. IEEE Access, 6, 15494–15504.
-
Ananthi, S., & Dhanalakshmi, P. (2013). Speech recognition system and isolated word recognition based on Hidden Markov model (HMM) for Hearing Impaired. International Journal of Computer Applications, 73(20), 30–34.
-
Aquino, G., Rubio, J. D. J., Pacheco, J., Gutierrez, G. J., Ochoa, G., Balcazar, R., Cruz, D. R., Garcia, E., Novoa, J. F., & Zacarias, A. (2020). Novel nonlinear hypothesis for the delta parallel robot modeling. IEEE Access, 8, 46324–46334.
-
Ashfahani, A., Pratama, M., Lughofer, E., & Ong, Y. S. (2020). DEVDAN: Deep evolving denoising autoencoder. Neurocomputing, 390, 297–314.
-
Bengio, Y. (2012). Practical recommendations for gradient-based training of deep architectures. In Neural networks: Tricks of the trade (pp. 437–478). Springer, Berlin
-
Chiang, H. S., Chen, M. Y., & Huang, Y. J. (2019). Wavelet-based EEG processing for epilepsy detection using fuzzy entropy and associative petri net. IEEE Access, 7, 103255–103262.
-
de Jesús Rubio, J. (2009). SOFMLS: Online self-organizing fuzzy modified least-squares network. IEEE Transactions on Fuzzy Systems, 17(6), 1296–1309.
-
Dhanashri, D., and Dhonde, S.B. (2017). Isolated word speech recognition system using deep neural networks. In Proceedings of the international conference on data engineering and communication technology (pp. 9–17). Springer, Singapore.
-
Elias, I., Rubio, J. D. J., Cruz, D. R., Ochoa, G., Novoa, J. F., Martinez, D. I., Muñiz, S., Balcazar, R., Garcia, E., & Juarez, C. F. (2020). Hessian with mini-batches for electrical demand prediction. Applied Sciences, 10(6), 2036.
-
Garofolo, J.S., Lamel, L.F., Fisher, W.M., Fiscus, J.G., and Pallett, D.S. (1993). DARPA TIMIT acoustic-phonetic continuous speech corpus CD-ROM. NIST speech disc 1–1.1. STIN, 93, p.27403.
-
Harik, G. R., Lobo, F. G., & Goldberg, D. E. (1999). The compact genetic algorithm. IEEE Transactions on Evolutionary Computation, 3(4), 287–297.
-
Jain, M., Gupta, M., and Jain, N. (2012). Linear phase second-order recursive digital integrators and differentiators. Radioengineering, 21(2).
-
Jain, M., Gupta, M., & Jain, N.K. (2013). Analysis and design of digital IIR integrators and differentiators using minimax and pole, zero, and constant optimization methods. ISRN Electronics, 2013.
-
Jain, M., & Shukla, S. (2019). Accurate speech emotion recognition by using brain-inspired decision-making spiking neural network. International Journal of Advanced Computer Science and Applications, 10, 12.
-
Kamalvir, K. P., & Neelu, J. (2015). A review of techniques used in the spoken-word recognition system. International Journal of Modern Engineering Research, 5(2), 23–27.
-
Karaboga, D., & Basturk, B. (2007). A powerful and efficient algorithm for numerical function optimization: artificial bee colony (ABC) algorithm. Journal of Global Optimization, 39(3), 459–471.
-
LeCun, Y.A., Bottou, L., Orr, G.B. and Müller, K.R. (2012). Efficient backprop. In Neural networks: Tricks of the trade (pp. 9–48). Springer, Berlin
-
Ma, X., and Zhou, W. (2008). AMS based spectrum subtraction algorithm with confidence interval test. In 7th Asian-Pacific Conference on Medical and Biological Engineering (pp. 389–391). Springer, Berlin, Heidelberg.
-
Meda-Campaña, J. A. (2018). On the estimation and control of nonlinear systems with parametric uncertainties and noisy outputs. IEEE Access, 6, 31968–31973.
-
Mirjalili, S., & Lewis, A. (2016). The whale optimization algorithm. Advances in Engineering Software, 95, 51–67.
-
Nawi, N. M., Khan, A., & Rehman, M. Z. (2013). CSLM: Levenberg marquardt based back propagation algorithm optimized with cuckoo search. Journal of ICT Research and Applications, 7(2), 103–116.
-
Oh, S. Y., & Chung, K. (2014). Improvement of speech detection using ERB feature extraction. Wireless Personal Communications, 79(4), 2439–2451.
-
Rabiner, L. R., & Juang, B. H. (1999). Fundamentals of speech recognition. Beijing: Tsinghua University Press.
-
Rabiner, L. R., & Schafer, R. W. (2005). Digital processing of speech signals. London: Pearson Education.
-
Selvaraj, L., & Balakrishnan, G. (2014). Enhancing speech recognition using improved particle swarm optimization based hidden Markov model. The Scientific World Journal, 2014, 1–10.
-
Shukla, S., & Jain, M. (2019). A novel system for effective speech recognition based on artificial neural network and opposition artificial bee colony algorithm. International Journal of Speech Technology, Springer, 22, 959–969.
-
Shukla, S., and Jain, M. (2020). A novel stochastic deep conviction network for emotion recognition in a speech signal. Journal of Intelligent & Fuzzy Systems, 38(4) , 5175–5190.
-
Shukla, S., Jain, M., & Dubey, R. K. (2019). Increasing the performance of speech recognition systems by using different optimization techniques to redesign artificial neural networks. Journal of Theoretical and Applied Information Technology, 97(8), 2404–2415.
-
Zhou, C., Gao, H. B., Gao, L., & Zhang, W. G. (2003). Particle swarm optimization (PSO) algorithm. Application Research of Computers, 12, 7–11.
normanoushavinge95.blogspot.com
Source: https://link.springer.com/article/10.1007/s10772-021-09851-x
0 Response to "What Makes Recognizing Continuous Speech More Di Cult Than Recognizing Isolated Words"
Post a Comment